基本数据结构整理

顺序结构

顺序栈

template <class T>
class sq_stack{
private:
    T val;
    int top;
    int size;
public:
    sq_stack();
    ~sq_stack();
    T pop();
    void insert(T val);
    int get_size(sq_stack s);
}

队列

template<class T>
class sq_queue{
private:
    T val;
    int front;
    int rear;
    int maxsize;
public:
    sq_queue();
    ~sq_queue();
    int get_rear(sq_queue r);
    int get_front(sq_queue f);
    void insert(T val);
}

顺序表

template <class T>
class sq_list{
    vector<T> a;
    int length;
    int size;
}

链式结构

##

template <class T>
class link_node{
private:
    T data;
    link_node *next;
public:
    link_node(T d):data(d),next(nullptr){}
    ~link_node();
}
typedef struct Lnode{
    elemtype data;
    struct Lnode *next;
}Lnode,*LinkList;

哈希表

• 哈希函数：H(key): K -> D , key ∈ K

• 构造方法

  1. 直接定址法
  2. 除留余数法
  3. 数字分析法
  4. 折叠法
  5. 平方取中法

• 冲突解决方法
  链地址法：key相同用单链表链接
  开放定址法：

• 线性探测法：放到key的下一个位置，Hi = (H(key) + i) % m

• 二次探测法：Hi = (H(key) + i) % m

• 随机探测法：Hi= (H(key) + 伪随机数) % m

typedef char KeyType;

typedef struct{
    KeyType key;
}RcdType;

typedef struct{
    RcdType *rcd;
    int size;
    int count;
    bool *tag;
}HashTable;

🌲

二叉🌲

存储结构

1. 顺序存储
2. 链式存储

   遍历方式

3. 先序
4. 后序
5. 中序
6. 层次

   实现

   template <class T>
   class binary_node{
   private:
       binary_node *left;
       binary_node *right;
       T val;
   public:
       binary_node(int x):val(x),left(nullptr),right(nullptr){}
       ~binary_node();
       void in_order(binary_node *root);
       void pre_order(binary_node *root);
       void post_order(binary_node *root);
       void level_order(binary_node *root);
   }

类型

• 满二叉🌲
• 完全二叉🌲(堆)
  • 大根堆
  • 小根堆
• 二叉查找🌲(排序🌲)
  1. 左子树上所有结点的值均小于或等于它的根结点的值。
  2. 右子树上所有结点的值均大于或等于它的根结点的值。
  3. 左、右子树也分别为二叉排序树。
  • 查找的最大次数等于数的高度。缺点(多次插入偏向一边的数据，会导致🌲严重不平衡)
• 平衡二叉🌲(AVL)

1. 平衡因子BF 左高-右高 ,根节点BF>1 右旋 顺时针 <-1 左旋
2. 插入结点后，最小不平衡子树的BF与它的子树的BF符号相反时，就需要对结点先进行一次旋转以使得符号相同后，再反向旋转一次才能够完成平衡操作

• 最小失衡🌲(平衡二叉树插入新的节点导致失衡的子🌲):调整策略

  • LL 左孩子右旋
  • RR 右孩子左旋
  • LR 左孩子左旋，再右旋
  • RL 右孩子的左子🌲先右旋，在左旋

    红黑🌲

    解决了二叉查找树的不平衡问题。最大查找次数不会超过最短路径的两倍。主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率高。
  1. 节点是红色或黑色。
  2. 根节点为黑色。
  3. 所有的叶子节点都是黑色的空节点。
  4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)。
  5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

     自平衡

  • 变色

  • 旋转
    左旋转
    逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子。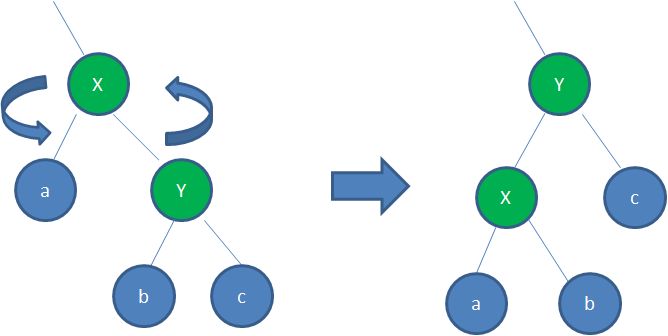
    

    右旋转
    顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子。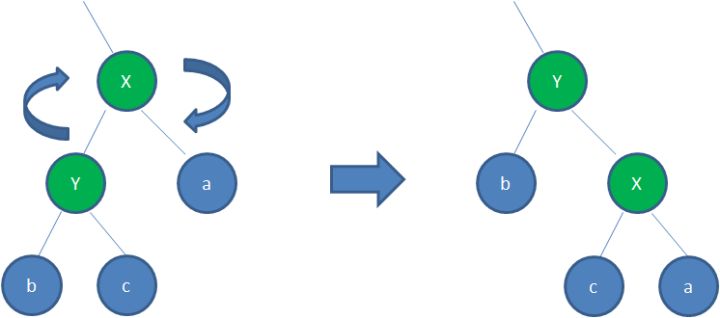
    

    实现

    enum tree_color(RED,BLACK);
    template <class T>
    class rb_node{
    public:
        tree_color color;
        T key;
        rb_node *left;
        rb_node *right;
        rb_node *parent;
        rb_node(T val,rb_color c,rb_node l,rb_node r,rb_node p):key(val),color(c),left(l),right(r),parent(p){}
    };
    template <class T>
    class rb_tree{
        rb_tree();
        ~rb_tree();
        void pre_order();   
        void in_order();
        void post_order();
        rb_node<T>* re_search(T key); //递归查找
        rb_node<T>* iter_serach(T key); //非递归
        T minkey();
        T maxkey();
        rb_node<T>* successor(rb_node<T> *x);
        rb_node<T>* predecessor(rb_node<T> *x);
        void insert(T key);
        void remove(T key);
        void destory();
        void print();
    private:
        void left_rotate(rb_node<T>* &root,rb_node<T>* &x);
        void right_rotate(rb_node<T>* &root,rb_node<T>* &x);
    }
    
    ## B🌲
    * m阶B🌲
        1.  每个结点最多有m-1个关键字
        2.  根结点最少可以只有1个关键字
        3.  每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它
        4.  根结点到每个叶子结点高度相同
        5.  非根结点至少有Math.ceil(m/2)-1个关键字
    
    ### 实现
    ```c++
    template <class T>
    struct B_tree_node {
        int n;
        vector<T> *key;
        bool is_leaf;
        struct B_tree_node *parent;
        vector<B_tree_node *> *child;
    };
    
    template <class T>
    class B_tree{
    private:
        B_tree_node<T>* root;
        int m;
    public:
        B_tree(int tVal = 2);
        ~B_tree();
        B_tree_node<T>* search_tree(B_tree_node<T>* root, T k ,int &index);
        B_tree_node<T>* getRoot();
        void insert(B_tree_node<T>* root,B_tree_node<T>* node);
        void delete(B_tree_node<T>* root,B_tree_node<T>* node);
        T get_value(B_tree_node<T>* root,T value);
    };

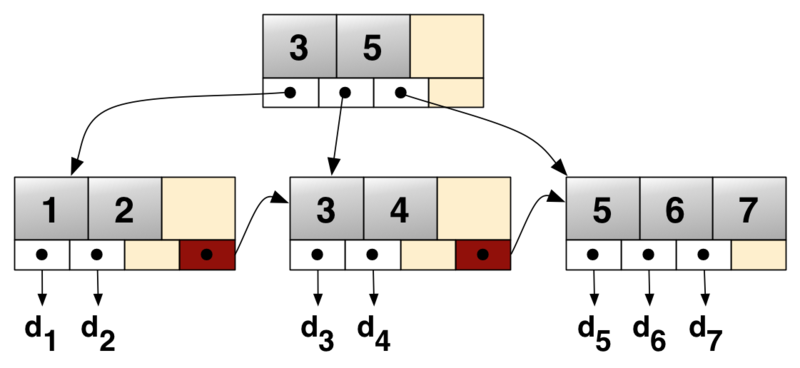
B+

• M阶B+🌲
  1. 内结点存有关键字和指向孩子结点指针。外结点存有关键字和数据。
  2. 叶子结点还有关键字，按照关键字大小排序，叶子结点中存在指向兄弟结点的指针。
  3. 一颗B+🌲存在两个指针，一个指向根结点，一个指向存有最小关键字的结点。
  4. 有n棵子树的结点中含有n个关键字，每个关键字不保存数据，只用来索引。
  5. 所有数据均存储在叶子结点中。
     

     template <class T>
     class bp_node{
         public:
         bp_node();
         virtual ~bp_node();
         private:
         T data;
     };
     template <class T>
     class inter_node: public bp_node{
         public:
     }

八叉树

图

排序

查找

递归

折半查找

归并查找

快速排序

迭代

折半查找

归并查找